
En defensa de la mecanización
En este vídeo, haremos una reflexión sobre si realmente es tan malo mecanizar en matemática, o si realmente tiene algun beneficio.

En este vídeo, haremos una reflexión sobre si realmente es tan malo mecanizar en matemática, o si realmente tiene algun beneficio.

En este vídeo, realizare una reflexión sobre mi participación en el Math Rocks Fest 2.0 y los eventos de divulgación de ciencia en general.

En este vídeo veremos cuales son las razones por las cuales un matemático podría convertirse en famoso.

En este vídeo, hablaremos sobre las distintas formas de dar clase que pueden tener los profesores universitarios. Si están mas orientados a la pedagogía o

En este vídeo veremos los problemas que tienen los vídeos cortos de Tik Tok, reels y shorts matemáticos.

En este vídeo vamos a discutir, que ocurre si uno se estudia un libro entero, estudiando toda la parte teórica y toda la parte practica,

En este vídeo veremos mi experiencias en las primeras materias de la carrera de la matemática en la Universidad de Buenos Aires.

En este vídeo veremos el famoso problema de la física que involucra una fuerza entre tres cuerpos desde el punto de vista de la mecánica

En este vídeo haremos una reseña a un libro clásico escrito por Hardy sobre lo que significa hacer matemática, «Apología de un matemático».

En este nuevo vídeo, veremos un recorrido por la carrera de matemática de la Universidad de Buenos Aires.

En este vídeo veremos una discusión sobre las dificultades de hacer divulgación de matemática en youtube.

En este vídeo veremos que es un congreso de matemática, en que consiste y que cosas se hacen en ellos.

En este vídeo, veremos la materia mas difícil que me ha tocado cursar en la carrera, repasando todas las materias de matemática y sus dificultades.

En este vídeo, veremos ejemplos de matemáticos considerados genios por sus logros, como hacen preguntas a colegas sobre temas específicos. Las discusiones académicas puestas en

En este vídeo veremos, los recursos mas importantes para aquellos estudiantes que quieran estudiar matemática por su cuenta.

En este vídeo veremos, un repaso de los temas mas importantes y básicos para el estudiante de matemática autodidacta.

En este vídeo explicaremos la equivalencia de la hipótesis de Riemann en la que trabajó el matemático Terence Tao.

En este vídeo veremos la opinión que da el gran matemático Terence Tao, sobre como demostrar la hipótesis de Riemann, como respuesta a una pregunta

En este vídeo veremos la demostración de la famosa fórmula de Euler usando series de potencia de funciones trigonométricas.
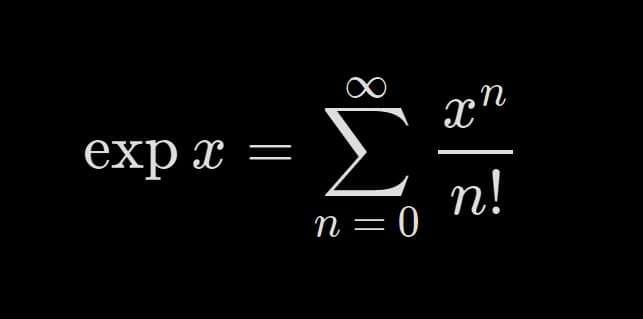
En este vídeo veremos como se puede demostrar que la serie definida como e a la x, efectivamente es convergente.
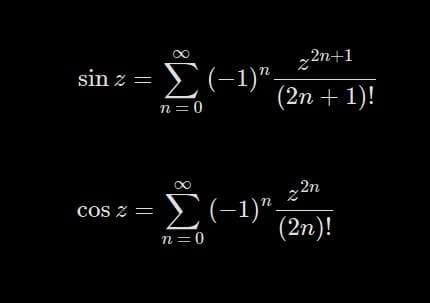
En este vídeo, veremos la demostración de la convergencia absoluta de las series de seno y coseno en los complejos. Estas series son muy importantes

En este vídeo veremos como podemos demostrar de varias formas, la fórmula para los primeros n números naturales.

En este vídeo intentaremos responder algunas preguntas matemáticas que pueden parecer absurdas, pero tienen un trasfondo interesante.

En este vídeo, veremos los principios filosóficos detrás de uno de los trabajos científicos mas importantes de la historia, el Principia de Newton.
En este vídeo veremos, contrario a lo que muchos piensan, fórmulas para obtener raíces de polinomios de grado mayor o igual a 5.

En este vídeo, veremos como podemos aproximar el número pi utilizando Excel y un modelo probabilístico.

En este vídeo, veremos unos números muy importantes en cuanto a la abundancia, los números colosalmente abundantes, relacionados con la hipótesis de Riemann y la

En este vídeo, seguimos con las comparaciones de los aleatorios, en este caso con el Wolfram Alpha.