En este vídeo veremos algo que no hemos visto mucho en el canal, un video sobre el terraplanismo. Específicamente las 10 cosas que los terraplanistas
En este vídeo veremos a un Sean Carroll hablando sobre las teorías alternativas a las estándares en la física en general.
En este vídeo hablaremos sobre la reciente noticia, de que un asteroide podría chocar con la tierra en 2032. Analizaremos directamente el reporte de la
En este vídeo veremos, la opinión de Penrose sobre el problema de la medición, un problema muy importante de la mecánica cuántica al día de
En este vídeo veremos a Leonard Susskind hablando del estado de las ideas sobre teoría de Cuerdas y el mundo de la física en general.
En este vídeo veremos la reseña a una obra que cambio el rumbo de la humanidad para siempre. El Philosophiae Naturalis Principia Mathematica de Newton.
En este vídeo veremos a Penrose hablando de si existen fenómenos que no podrán ser testeados científicamente en el futuro.
En este vídeo, veremos la opinión de Sabine Hossenfelder relacionado con la testeabilidad de las teorías y la teoría de cuerdas.
En este vídeo, veremos la opinión de Sabine Hossenfelder, sobre el multiverso, ya que es una física crítica sobre la teoría en general.
En este vídeo veremos, a Leonard Susskind hablando sobre si el universo esta tuneado, es decir tiene las condiciones iniciales para la aparición de la
En este vídeo, veremos al físico Lee Smolin hablando sobre si el espacio y el tiempo son fundamentales en el sentido de que podemos entender
En este vídeo reaccionaremos al físico Leonard Susskind hablando sobre agujeros negros y mecánica cuántica.
En este video, veremos a un Medallista Fileds Cedric Villani, hablando sobre las grandes mentes de la ciencia.
En este vídeo, veremos una charla de Terence Tao hablando sobre como la IA puede ayudar al progreso de la ciencia en general.
En este vídeo, reaccionaremos a Andrew Wiles y su comentario sobre la solución del último teorema de Fermat
En este vídeo, veremos el debate y opinión de físicos sobre el estado de la teoría de cuerdas, si es que esta en declive, en
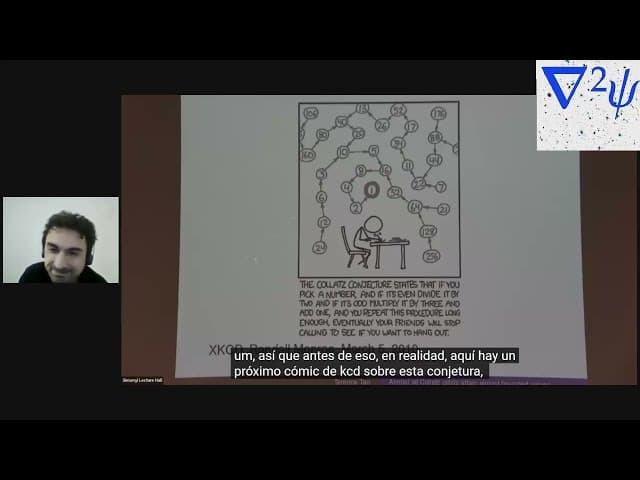
En este vídeo veremos el principio de la charla que dio Terence Tao sobre sus avances en la Conjetura de Collatz.
En este vídeo, veremos la opinión de Andrew Wiles, el matemático que demostró el último teorema de Fermat, sobre si la matemática se descubre o
En este vídeo, veremos la reacción a la opinión de Andrew Wiles sobre la creatividad en la matemática.
En este vídeo, veremos la opinión de Terence Tao sobre como hacer matemática en tiempos de internet.
En este vídeo, veremos la opinión, del físico Leonard Susskind hablando sobre por qué la matemática funciona para explicar el universo.
En este vídeo reaccionaremos a una charla de Tao sobre los avances en la conjetura de los Primos Gemelos.
En este vídeo veremos una reacción a la primer parte de la charla que dio James Maynard sobre los nuevos avances en la hipótesis de
En este vídeo veremos nuevos resultados de 2024, para la hipotesis de Riemann, por el gran matemático James Maynard.
En este vídeo analizaremos un mapa de la carrera de la matemática enviado por un suscriptor.
En este vídeo veremos como son los pasos para poder escribir un artículo matemático.
En este vídeo veremos cuales son las posibilidades para un estudiante o egresado de la carrera de matemática, ya sea profesor o licenciado.
En este vídeo veremos si cualquier persona puede publicar un artículo científico matemático o si hay ciertas condiciones que se debe cumplir para ello.
