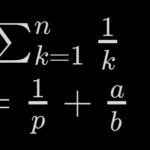Las sumas parciales de la serie armónica no son enteros demostración con el postulado de Bertrand

Retomando lo visto en el vídeo anterior, vamos a ver que las sumas parciales de la serie armónica nunca son un número entero, pero ahora la demostración será distinta. Vamos a utilizar el postulado de Bertrand  que nos dice que entre cualquier número mayor que 1 y su doble, por lo menos existe un número primo. Por ejemplo entre 3 y 6 está el primo 5. De esta forma, veremos que podemos llegar por varios caminos a un mismo resultado.